Interesting facts: Rational and irrational polygons

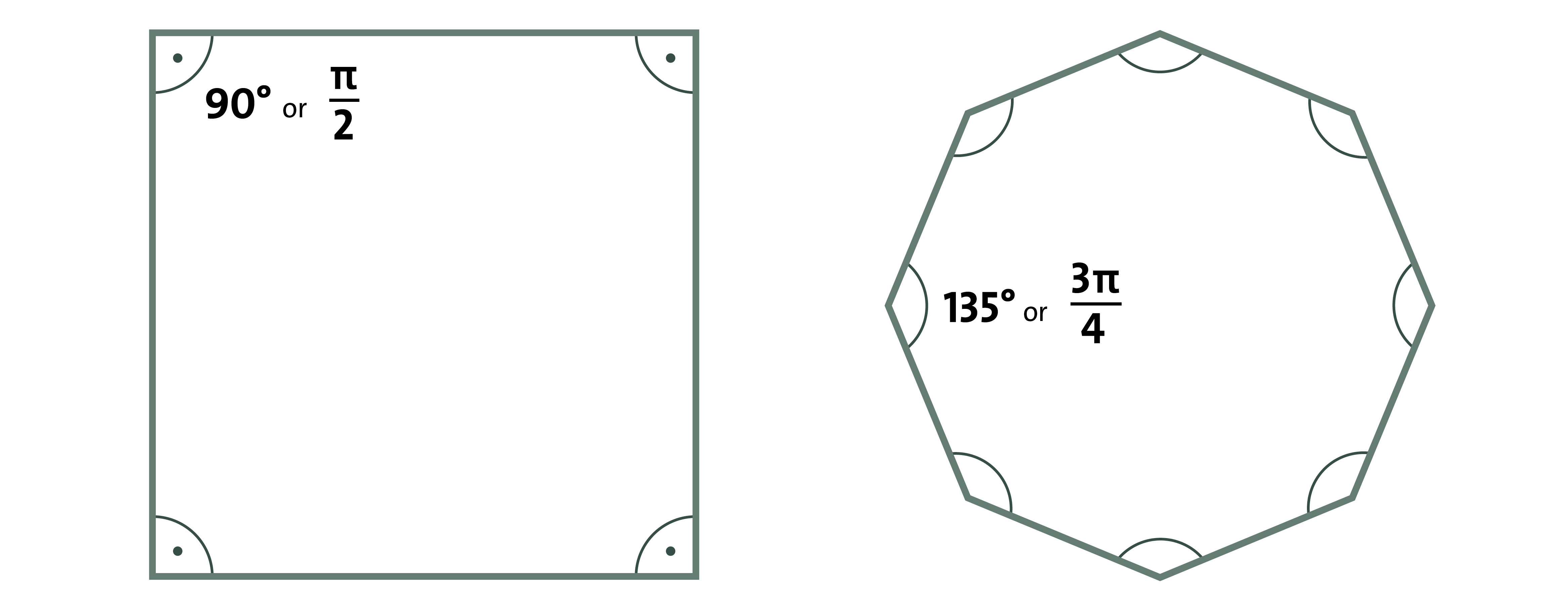
Polygons that can be unfolded to a surface, e.g. that of a pretzel, are what mathematicians call rational polygons. Their angles are all fractions of the full angle 360°.

Angles in mathematics are measured from 0 to 2π rather than 0 to 360° as in everyday life. Pi (π) is a mathematical constant and equals approximately 3.14159265358979323846…

Thus, all angles of rational polygons are fractions of the full 2π (360°) angle, e.g. π/2, π/8, 3/4π, etc.

A rectangle, for example, is a rational polygon because it has four π/2 angles (right angles, 90°), but a regular octagon is also a rational polygon since all its angles are 3π/4

Polygons with irrational angles (which are not fractions of 2π) can be unfolded. However, they give rise to infinite surfaces, i.e. surfaces which extend indefinitely in space or otherwise present difficulties.

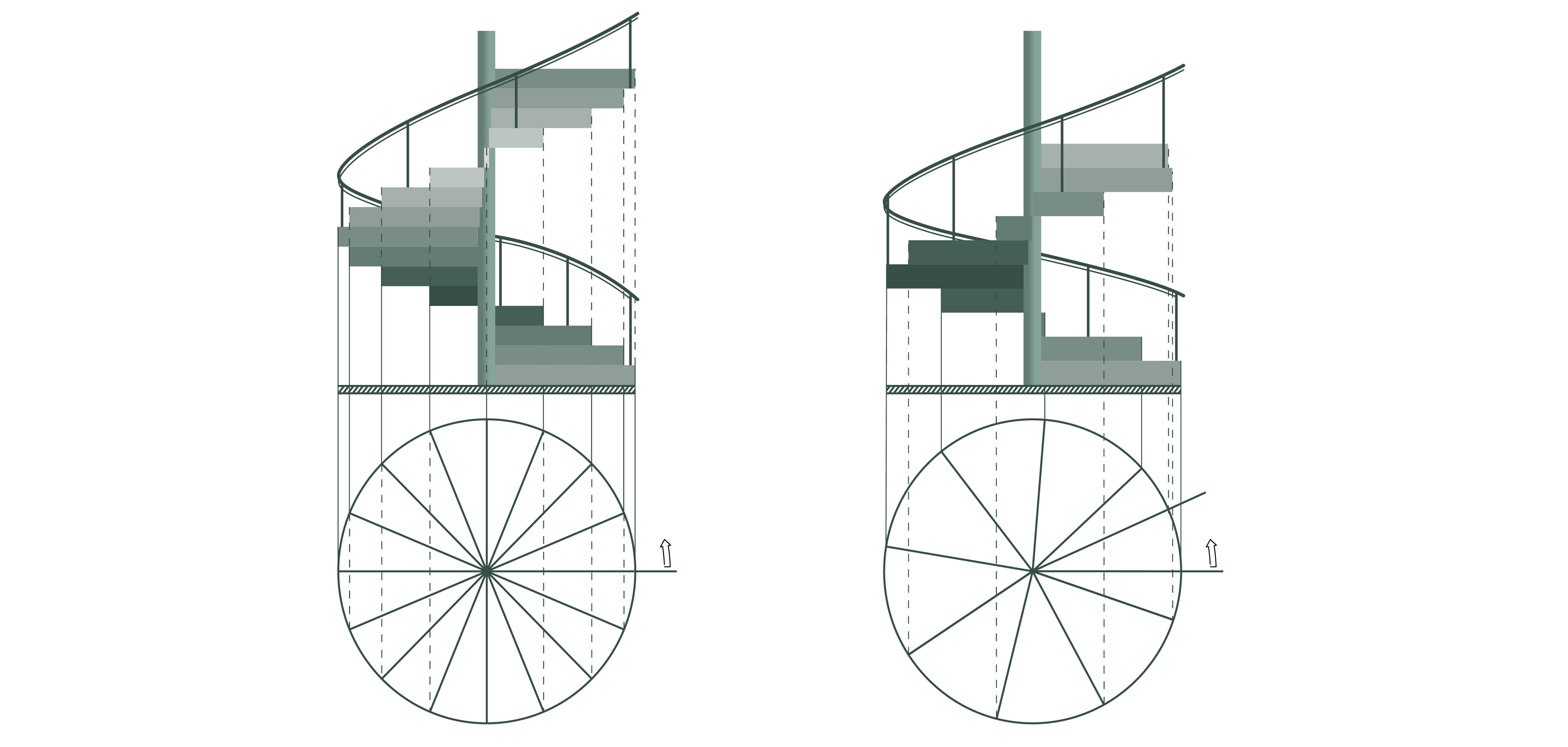
The treads of a rational spiral staircase do not overlap; those of an irrational one do.

Trajectories and chaotic properties of rational polygons are well understood by mathematicians thanks to the powerful tools found in an area of research called Teichmüller dynamics.

We know very little about irrational polygons and billiard tables of this shape: even a simple question such as ‘is there a periodic trajectory on every such table?’ remains unanswered to this day.