Interessant zu wissen: Rationale und irrationale Polygone

Polygone, die zu einer Fläche wie die eines Brezels entfaltet werden können, nennen Mathematiker*innen rationale Polygone. Das sind Polygone, dessen Winkel Bruchteile von Vollwinkels 360° sind.

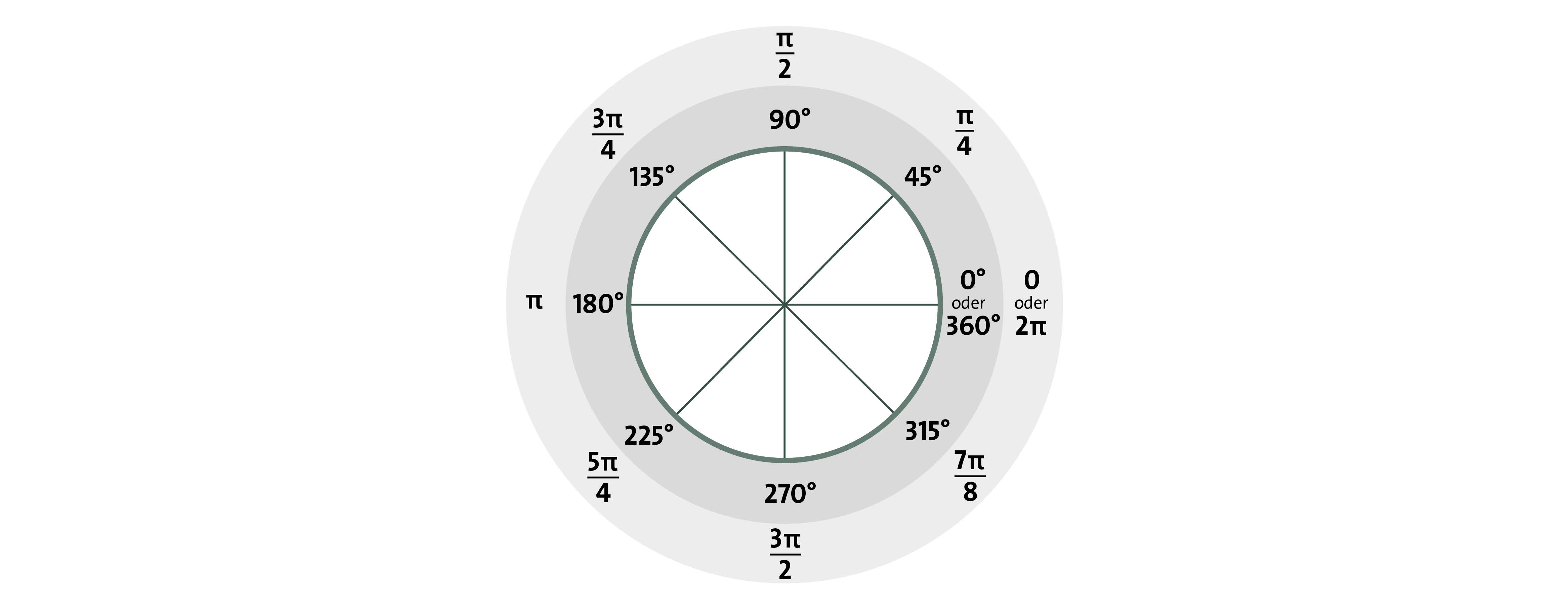
Wenn in der Mathematik über Winkel geredet wird, misst man diese von 0 bis 2π und nicht wie im Alltag von 0 bis 360°. Dabei ist π die Kreiszahl 3.14159265358979323846… .

Alle Winkel rationaler Polygone sind Bruchteile des ganzen 2π (360°) Winkels, z.B. π/2, π/8, 3/4π, etc.

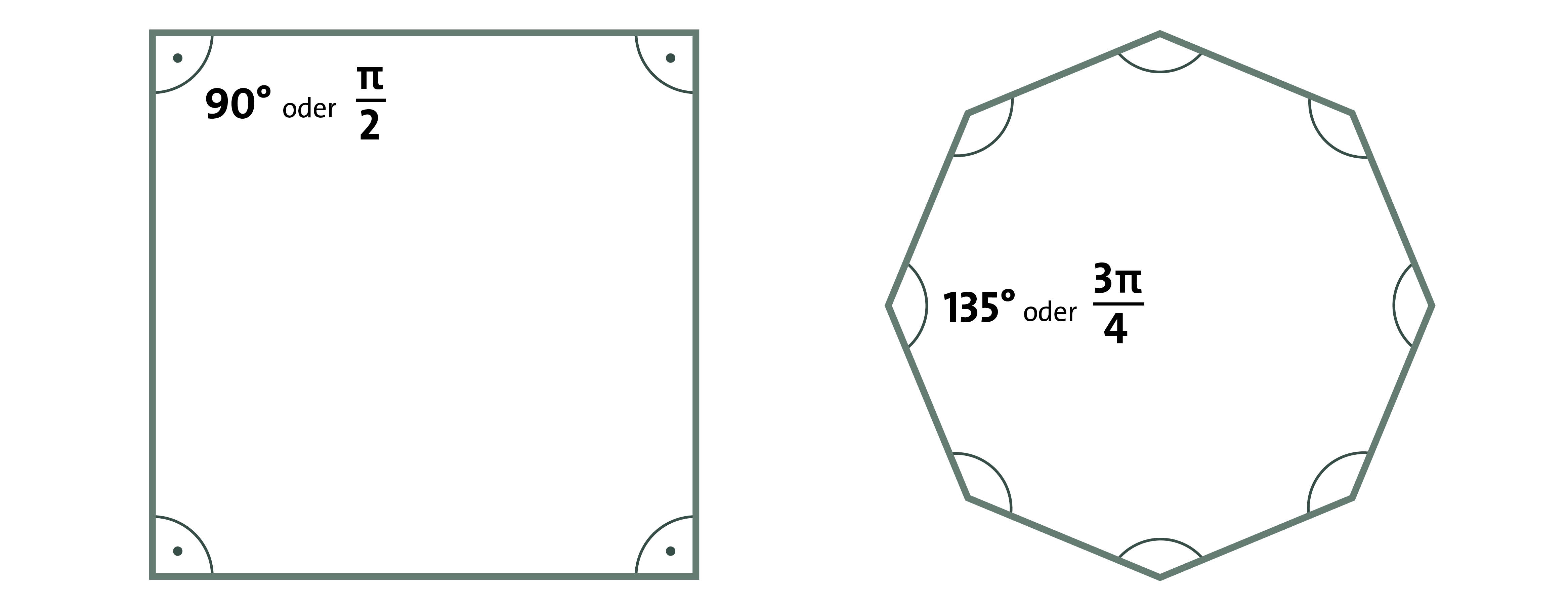
Das Rechteck z. B. ist ein rationales Polygon, weil es vier π/2 Winkel (rechte Winkel, 90°) hat. Aber auch ein reguläres Achteck ist ein rationales Polygon, denn alle seine Winkel sind 3π/4.

Auch Polygone mit irrationalen Winkeln (die nicht Bruchteile von 2π sind) können entfaltet werden. Sie führen jedoch zu unendlichen Flächen – d. h. Flächen, welche sich räumlich unendlich erstrecken oder sonstige Schwierigkeiten aufweisen.

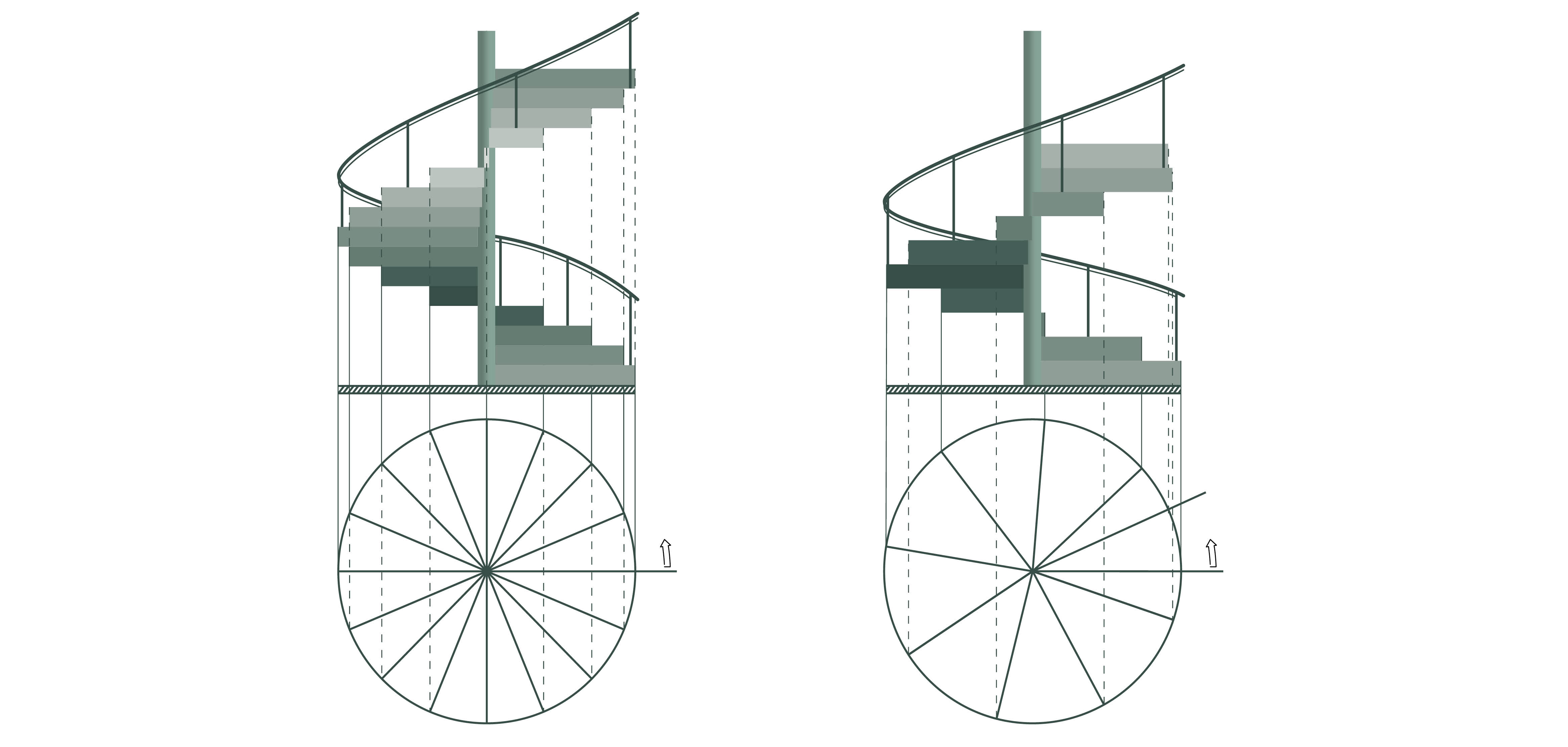
Bei einer rationalen Wendeltreppe überschneiden sich die Stufen nicht, bei einer irrationalen schon.

Die Spuren und chaotischen Eigenschaften rationaler Polygone werden von den Mathematiker*innen dank der leistungsfähigen mathematischen Werkzeuge der sogenannten «Teichmuller Dynamik» Forschungsgebiet gut verstanden.

Wir wissen sehr wenig über irrationale Polygone und Billardtische dieser Form: Selbst auf eine Grundfrage wie «Gibt es eine periodisch verlaufende Spur auf jedem dieser Tische?» gibt es noch immer keine Antwort.